Electromagnetic Field: July 2011

Friday 1 July 2011

Tips for keeping the FeedBulletin feed private

Electromagnetic field

From Wikipedia, the free encyclopedia

Electromagnetism

Electricity · Magnetism

[show]Electrostatics

[show]Magnetostatics

[hide]Electrodynamics
Lorentz force law · emf · Electromagnetic induction · Faraday’s law · Lenz's law · Displacement current · Maxwell's equations · EM field · Electromagnetic radiation · Liénard–Wiechert potential · Maxwell tensor · Eddy current

[show]Electrical Network

[show]Covariant formulation

[show]Scientists

An electromagnetic field (also EMF or EM field) is a physical field produced by electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction. It is one of the four fundamental forces of nature (the others are gravitation, the weak interaction, and the strong interaction).
The field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, and the magnetic field by moving charges (currents); these two are often described as the sources of the field. The way in which charges and currents interact with the electromagnetic field is described by Maxwell's equations and the Lorentz force law.
From a classical perspective, the electromagnetic field can be regarded as a smooth, continuous field, propagated in a wavelike manner; whereas from the perspective of quantum field theory, the field is seen as quantized, being composed of individual particles.^{[citation needed]}

Structure of the electromagnetic field

The electromagnetic field may be viewed in two distinct ways: a continuous structure or a discrete structure.

Continuous structure

Classically, electric and magnetic fields are thought of as being produced by smooth motions of charged objects. For example, oscillating charges produce electric and magnetic fields that may be viewed in a 'smooth', continuous, wavelike fashion. In this case, energy is viewed as being transferred continuously through the electromagnetic field between any two locations. For instance, the metal atoms in a radio transmitter appear to transfer energy continuously. This view is useful to a certain extent (radiation of low frequency), but problems are found at high frequencies (see ultraviolet catastrophe).

Discrete structure

The electromagnetic field may be thought of in a more 'coarse' way. Experiments reveal that in some circumstances electromagnetic energy transfer is better described as being carried in the form of packets called quanta (in this case, photons) with a fixed frequency. Planck's relation links the energy

E

of a photon to its frequency

ν

through the equation:

$E= \, h \, \nu$

where

h

is Planck's constant, named in honor of Max Planck, and

ν

is the frequency of the photon . Although modern quantum optics tells us that there also is a semi-classical explanation of the photoelectric effect —the emission of electrons from metallic surfaces subjected to electromagnetic radiation— the photon was historically (although strictly unnecessarily) used to explain certain observations. It is found that increasing the intensity of the incident radiation (so long as one remains in the linear regime) increases only the number of electrons ejected, and has almost no effect on the energy distribution of their ejection. Only the frequency of the radiation is relevant to the energy of the ejected electrons.
This quantum picture of the electromagnetic field (which treats it as analogous to harmonic oscillators) has proved very successful, giving rise to quantum electrodynamics, a quantum field theory describing the interaction of electromagnetic radiation with charged matter. It also gives rise to Quantum optics, which is different from quantum electrodynamics in that the matter itself is modelled using quantum mechanics rather than Quantum field theory

The electromagnetic field as a feedback loop

The behavior of the electromagnetic field can be resolved into four different parts of a loop:

the electric and magnetic fields are generated by electric charges,
the electric and magnetic fields interact only with each other,
the electric and magnetic fields produce forces on electric charges,
the electric charges move in space.

A common misunderstanding is that the quanta in the field are the same as the charged particles that generate the fields. In our everyday world, charged particles, such as electrons, move slowly through matter typically on the order of a few inches (or centimeters) per second^{[citation needed]}, but fields propagate at the speed of light - approximately 186 thousand miles (or 300 thousand kilometers) a second. The mundane speed difference between charged particles and field quanta is on the order of one to a million, more or less. Maxwell's equations relate the presence and movement of charged particles with the generation of fields, that can then affect the force on, and move, other slowly moving charged particles. Charged particles can move at relativistic speeds nearing field propagation speeds, but, as Einstein showed^{[citation needed]}, this requires enormous field energies, which are not present in our everyday experiences with electricity, magnetism, matter, and time.
The feedback loop can be summarized in a list, including phenomena belonging to each part of the loop:

charged particles generate electric and magnetic fields
the fields interact with each other
- changing electric field acts like a current, generating 'vortex' of magnetic field
- Faraday induction: changing magnetic field induces (negative) vortex of electric field
- Lenz's law: negative feedback loop between electric and magnetic fields
fields act upon particles
- Lorentz force: force due to electromagnetic field
  - electric force: same direction as electric field
  - magnetic force: perpendicular both to magnetic field and to velocity of charge
particles move
- current is movement of particles
particles generate more electric and magnetic fields; cycle repeats

Mathematical description

Main article: Mathematical descriptions of the electromagnetic field

There are different mathematical ways of representing the electromagnetic field. The first one views the electric and magnetic fields as three-dimensional vector fields. These vector fields each have a value defined at every point of space and time and are thus often regarded as functions of the space and time coordinates. As such, they are often written as $\mathbf{E}(x, y, z, t)$ (electric field) and $\mathbf{B}(x, y, z, t)$ (magnetic field).
If only the electric field ( 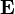$\mathbf{E}$ ) is non-zero, and is constant in time, the field is said to be an electrostatic field. Similarly, if only the magnetic field ( $\mathbf B$ ) is non-zero and is constant in time, the field is said to be a magnetostatic field. However, if either the electric or magnetic field has a time-dependence, then both fields must be considered together as a coupled electromagnetic field using Maxwell's equations.^[1]
With the advent of special relativity, physical laws became susceptible to the formalism of tensors. Maxwell's equations can be written in tensor form, generally viewed by physicists as a more elegant means of expressing physical laws.
The behaviour of electric and magnetic fields, whether in cases of electrostatics, magnetostatics, or electrodynamics (electromagnetic fields), is governed in a vacuum by Maxwell's equations. In the vector field formalism, these are:

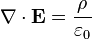$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$ (Gauss's law)

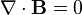$\nabla \cdot \mathbf{B} = 0$ (Gauss's law for magnetism)

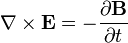$\nabla \times \mathbf{E} = -\frac {\partial \mathbf{B}}{\partial t}$ (Faraday's law)

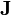$\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0\varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$ (Ampère-Maxwell law)

where

ρ

is the charge density, which can (and often does) depend on time and position,

ε 0

is the permittivity of free space,

μ 0

is the permeability of free space, and $\mathbf J$ is the current density vector, also a function of time and position. The units used above are the standard SI units. Inside a linear material, Maxwell's equations change by switching the permeability and permittivity of free space with the permeability and permittivity of the linear material in question. Inside other materials which possess more complex responses to electromagnetic fields, these terms are often represented by complex numbers, or tensors.
The Lorentz force law governs the interaction of the electromagnetic field with charged matter.
When a field travels across to different media, the properties of the field change according to the various boundary conditions. These equations are derived from Maxwell's equations. The tangential components of the electric and magnetic fields as they relate on the boundary of two media are as follows^[2]:

$\mathbf{E_{1}} = \mathbf{E_{2}}$

$\mathbf{H_{1}} = \mathbf{H_{2}}$ (current-free)

$\mathbf{D_{1}} = \mathbf{D_{2}}$ (charge-free)

$\mathbf{B_{1}} = \mathbf{B_{2}}$

The angle of refraction of an electric field between media is related to the permittivity $(\varepsilon)$ of each media:

$\frac{{\tan\theta_1}}{{\tan\theta_2}} = \frac{{\varepsilon_{r2}}}{{\varepsilon_{r1}}}$

The angle of refraction of an magnetic field between media is related to the permeability

(μ)

of each media:

$\frac{{\tan\theta_1}}{{\tan\theta_2}} = \frac{{\mu_{r2}}}{{\mu_{r1}}}$

Properties of the field

Reciprocal behavior of electric and magnetic fields

The two Maxwell equations, Faraday's Law and the Ampère-Maxwell Law, illustrate a very practical feature of the electromagnetic field Faraday's Law may be stated roughly as 'a changing magnetic field creates an electric field'. This is the principle behind the electric generator.
Ampere's Law roughly states that 'a changing electric field creates a magnetic field'. Thus, this law can be applied to generate a magnetic field and run an electric motor.

Light as an electromagnetic disturbance

Maxwell's equations take the form of an electromagnetic wave in an area that is very far away from any charges or currents (free space) – that is, where

ρ

and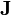 $\mathbf J$ are zero. It can be shown, that, under these conditions, the electric and magnetic fields satisfy the electromagnetic wave equation^[3]:

$\left( \nabla^2 - { 1 \over {c}^2 } {\partial^2 \over \partial t^2} \right) \mathbf{E} \ \ = \ \ 0$

$\left( \nabla^2 - { 1 \over {c}^2 } {\partial^2 \over \partial t^2} \right) \mathbf{B} \ \ = \ \ 0$

James Clerk Maxwell was the first to obtain this relationship by his completion of Maxwell's equations with the addition of a displacement current term to Ampere's Circuital law.

Relation to and comparison with other physical fields

Main article: Fundamental forces

This section requires expansion.

Being one of the four fundamental forces of nature, it is useful to compare the electromagnetic field with the gravitational, strong and weak fields. The word 'force' is sometimes replaced by 'interaction' because the fundamental forces operate by exchanging what are now known to be gauge bosons.

Electromagnetic and gravitational fields

Sources of electromagnetic fields consist of two types of charge – positive and negative. This contrasts with the sources of the gravitational field, which are masses. Masses are sometimes described as gravitational charges, the important feature of them being that there is only one type (no negative masses), or, in more colloquial terms, 'gravity is always attractive'.
The relative strengths and ranges of the four interactions and other information are tabulated below:

Theory	Interaction	mediator	Relative Magnitude	Behavior	Range
Chromodynamics	Strong interaction	gluon	10³⁸	1	10⁻¹⁵ m
Electrodynamics	Electromagnetic interaction	photon	10³⁶	1/r²	infinite
Flavordynamics	Weak interaction	W and Z bosons	10²⁵	1/r⁵ to 1/r⁷	10⁻¹⁶ m
Geometrodynamics	Gravitation	graviton	10⁰	1/r²	infinite