Properties of the field

Properties of the field

Reciprocal behavior of electric and magnetic fields

The two Maxwell equations, Faraday's Law and the Ampère-Maxwell Law, illustrate a very practical feature of the electromagnetic field Faraday's Law may be stated roughly as 'a changing magnetic field creates an electric field'. This is the principle behind the electric generator.
Ampere's Law roughly states that 'a changing electric field creates a magnetic field'. Thus, this law can be applied to generate a magnetic field and run an electric motor.

Light as an electromagnetic disturbance

Maxwell's equations take the form of an electromagnetic wave in an area that is very far away from any charges or currents (free space) – that is, where ρ and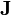 are zero. It can be shown, that, under these conditions, the electric and magnetic fields satisfy the electromagnetic wave equation^[3]:

James Clerk Maxwell was the first to obtain this relationship by his completion of Maxwell's equations with the addition of a displacement current term to Ampere's Circuital law.