Mathematical description
Main article: Mathematical descriptions of the electromagnetic field
There are different mathematical ways of representing the electromagnetic field. The first one views the electric and magnetic fields as three-dimensional vector fields. These vector fields each have a value defined at every point of space and time and are thus often regarded as functions of the space and time coordinates. As such, they are often written as  (electric field) and
(electric field) and  (magnetic field).
(magnetic field).If only the electric field (
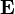 ) is non-zero, and is constant in time, the field is said to be an electrostatic field. Similarly, if only the magnetic field (
) is non-zero, and is constant in time, the field is said to be an electrostatic field. Similarly, if only the magnetic field ( ) is non-zero and is constant in time, the field is said to be a magnetostatic field. However, if either the electric or magnetic field has a time-dependence, then both fields must be considered together as a coupled electromagnetic field using Maxwell's equations.[1]
) is non-zero and is constant in time, the field is said to be a magnetostatic field. However, if either the electric or magnetic field has a time-dependence, then both fields must be considered together as a coupled electromagnetic field using Maxwell's equations.[1]With the advent of special relativity, physical laws became susceptible to the formalism of tensors. Maxwell's equations can be written in tensor form, generally viewed by physicists as a more elegant means of expressing physical laws.
The behaviour of electric and magnetic fields, whether in cases of electrostatics, magnetostatics, or electrodynamics (electromagnetic fields), is governed in a vacuum by Maxwell's equations. In the vector field formalism, these are:
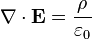 (Gauss's law)
(Gauss's law)
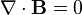 (Gauss's law for magnetism)
(Gauss's law for magnetism)
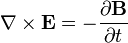 (Faraday's law)
(Faraday's law)
 (Ampère-Maxwell law)
(Ampère-Maxwell law)
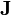 is the current density vector, also a function of time and position. The units used above are the standard SI units. Inside a linear material, Maxwell's equations change by switching the permeability and permittivity of free space with the permeability and permittivity of the linear material in question. Inside other materials which possess more complex responses to electromagnetic fields, these terms are often represented by complex numbers, or tensors.
is the current density vector, also a function of time and position. The units used above are the standard SI units. Inside a linear material, Maxwell's equations change by switching the permeability and permittivity of free space with the permeability and permittivity of the linear material in question. Inside other materials which possess more complex responses to electromagnetic fields, these terms are often represented by complex numbers, or tensors.The Lorentz force law governs the interaction of the electromagnetic field with charged matter.
When a field travels across to different media, the properties of the field change according to the various boundary conditions. These equations are derived from Maxwell's equations. The tangential components of the electric and magnetic fields as they relate on the boundary of two media are as follows[2]:
 (current-free)
(current-free)
 (charge-free)
(charge-free)
 of each media:
of each media:

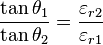

No comments:
Post a Comment